Aljabar: Pengertian, Bentuk, Rumus, hingga Contoh Soalnya

Yuk, pelajari apa itu aljabar, pengertian, bentuk, rumus, dan contoh soalnya untuk memahami dasar matematika dengan mudah!

—

Bayangkan kamu sedang berbelanja di pasar, membawa uang Rp100.000. Kamu ingin membeli buah, tapi belum tahu harganya pasti karena tergantung beratnya. Penjual berkata, “Harganya Rp15.000 per kilogram.” Saat itu tanpa sadar kamu sedang menggunakan konsep aljabar.

Kalimat seperti, “Rp15.000 per kilogram”, sebenarnya adalah hubungan antara harga dan berat. Inilah yang dijelaskan oleh aljabar, cabang matematika yang mempelajari hubungan antar variabel. Banyak orang bertanya, apa itu aljabar sebenarnya? Bukan sekadar kumpulan huruf dan angka rumit di papan tulis, aljabar justru membantu kita memahami pola, memprediksi hasil, dan menyelesaikan masalah nyata dalam kehidupan sehari-hari, dari menghitung ongkos hingga menentukan kecepatan kendaraan.

 

Penemu Aljabar

Muhammad ibn Musa Al-Khawarizmi, seorang matematikawan dan astronom Muslim Persia pada abad ke-9 Masehi, dikenal sebagai bapak aljabar dan juga penemu algoritma. Karya monumental Al-Khawarizmi adalah bukunya yang berjudul Al-Kitab al-Mukhtasar Fi Hisab al-Jabr wa’l-Muqabala. Dalam buku ini, Al-Khawarizmi memperkenalkan metode sistematis untuk menyelesaikan persamaan linear dan kuadrat, yang menjadi dasar dari cabang matematika yang kini dikenal sebagai aljabar.

Selain mengembangkan aljabar, Al-Khawarizmi juga dikenal sebagai penemu angka nol dan memberikan kontribusi penting dalam pengembangan tabel trigonometri dan ilmu hitung. Konsep dan istilah aljabar sendiri berasal dari kata Arab “al-jabr” yang terdapat dalam judul bukunya. Aljabar artinya “penggabungan” atau “penyempurnaan”. Karya dan pemikiran Al-Khawarizmi menjadi landasan penting dalam sejarah matematika dan mempengaruhi perkembangan matematika di Eropa serta dunia hingga saat ini.

Baca juga: Eksponen: Pengertian, Sifat, Fungsi, dan Contoh Soal 

 

Pengertian Aljabar

Aljabar adalah cabang ilmu matematika yang mempelajari simbol-simbol dan aturan operasi yang digunakan untuk memanipulasi simbol-simbol tersebut. Dalam aljabar, simbol-simbol seperti huruf (variabel) digunakan untuk mewakili angka atau nilai yang belum diketahui sehingga memudahkan dalam penyederhanaan dan pemecahan masalah matematika. 

Penggunaan aljabar mencakup penyelesaian persamaan dan fungsi, dengan bentuk-bentuk dasar seperti persamaan linear, persamaan kuadrat, dan polinomial. Aljabar menggeneralisasi operasi aritmetika seperti penjumlahan, pengurangan, perkalian, dan pembagian dengan menggunakan variabel.

 

Unsur-Unsur Aljabar

Unsur-unsur aljabar terdiri dari beberapa komponen utama yang membentuk ekspresi aljabar. Unsur ini penting untuk diketahui agar memahami cara kerja aljabar dalam matematika. Berikut adalah unsur-unsur dasar dalam aljabar.

1. Variabel

Variabel adalah simbol atau lambang, biasanya berupa huruf, yang mewakili nilai yang belum diketahui atau bisa berubah. Contohnya adalah x, y, a, b, dan sebagainya.

 

2. Koefisien

Koefisien dikenal sebagai angka yang mengalikan variabel dalam suatu suku aljabar. Misalnya, pada 3x, angka 3 adalah koefisien dari variabel x.

 

3. Konstanta 

Konstanta adalah nilai tetap berupa angka yang berdiri sendiri dalam bentuk aljabar tanpa variabel. Contohnya adalah angka 5 atau -9 dalam suatu ekspresi.

 

4. Suku 

Suku adalah bagian dari bentuk aljabar yang terdiri atas koefisien dan variabel atau hanya konstanta, yang dipisahkan oleh operasi penjumlahan atau pengurangan. Suku dapat berupa satu suku (monomial), dua suku (binomial), atau lebih.

 

Bentuk Aljabar

Ada beberapa jenis bentuk aljabar berdasarkan jumlah sukunya:

• Monomial: bentuk aljabar dengan satu suku, contohnya
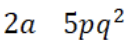
• Binomial: bentuk aljabar dengan dua suku, contohnya
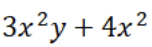
• Trinomial: bentuk aljabar dengan tiga suku, contohnya
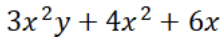
• Polinomial: bentuk aljabar dengan lebih dari tiga suku, contohnya

Unsur utama dalam bentuk aljabar meliputi konstanta (nilai tetap), variabel (nilai berubah-ubah), dan koefisien (angka pengali variabel). Dalam aljabar juga terdapat operasi-operasi seperti penjumlahan, pengurangan, perkalian, perpangkatan, dan pemfaktoran yang biasa diterapkan untuk menyelesaikan bentuk-bentuk aljabar tersebut.

Baca juga: Cara Mencari KPK dan FPB, Perbedaan & Contoh Soal 

 

Sifat Aljabar

Mari mengenal sifat-sifat aljabar sebelum kita lompat lebih jauh ke operasi bilangan.

1. Sifat Komutatif 

Hasil operasi penjumlahan atau perkalian tidak bergantung pada urutan bilangan. Contoh: a + b = b + a dan a . b = b . a

 

2. Sifat Asosiatif

Cara pengelompokan dalam penjumlahan atau perkalian tidak memengaruhi hasilnya. Contoh: (a + b) + c = a + (b + c) dan (a . b) . c = a . (b . c)

 

3. Sifat Distributif

Perkalian terhadap penjumlahan atau pengurangan dapat didistribusikan. Contoh: a . (b + c) = a . b + a . c

 

4. Sifat Identitas

Ada elemen identitas untuk penjumlahan dan perkalian yang tidak mengubah nilai suatu bilangan. Untuk penjumlahan elemen identitasnya adalah 0, dan untuk perkalian adalah 1.

5. Sifat Invers

Untuk setiap bilangan, terdapat bilangan invers yang jika dijumlahkan atau dikalikan akan menghasilkan elemen identitas. Invers penjumlahan dari a adalah -a, sedangkan invers perkalian dari a (dengan ) adalah .

 

Operasi Hitung dan Rumus Aljabar

Operasi hitung adalah serangkaian tindakan matematika dasar yang melibatkan bilangan dan digunakan juga dalam aljabar untuk mengelola dan menyelesaikan ekspresi atau persamaan. Empat operasi hitung dasar yang umum adalah:

1. Penjumlahan (+): Menggabungkan dua bilangan atau lebih menjadi satu nilai total.
2. Pengurangan (-): Mengurangi satu bilangan dari bilangan lain.
3. Perkalian (×): Penjumlahan berulang dari bilangan yang sama.
4. Pembagian (÷): Memisahkan bilangan menjadi bagian-bagian yang sama.

Dalam aljabar, operasi hitung ini diterapkan pada ekspresi yang mengandung variabel dan konstanta. Contohnya: 

• Penjumlahan dan pengurangan suku sejenis: 3x + 5x = 8x
• Perkalian menggunakan sifat distributif: a(b + c) = ab + ac
• Perpangkatan bentuk aljabar: (x + y)² = x² + 2xy + y²

 

Contoh Soal Aljabar

1. Menentukan nilai variabel

Soal:

Jika 2x + 5 = 11, maka nilai x adalah …

Penyelesaian:

2x = 11 – 5

2x = 6

x = 3

Jawaban: x = 3

 

2. Menyederhanakan bentuk aljabar

Soal:

Sederhanakan 3a + 4b – 2a + 5b

Penyelesaian:

Gabungkan suku sejenis:

(3a – 2a) + (4b + 5b) = a + 9b

Jawaban: a + 9b

 

3. Menghitung nilai bentuk aljabar

Soal:

Hitung nilai 4x – 3y jika x = 5 dan y = 2

Penyelesaian:

4(5) – 3 (2) = 20 – 6 = 14

Jawaban: 14

 

Turunan Fungsi Aljabar

Fungsi aljabar adalah suatu fungsi matematika yang dinyatakan dengan ekspresi aljabar yang terdiri dari variabel dan konstanta yang dihubungkan oleh operasi aljabar seperti penjumlahan, pengurangan, perkalian, pembagian, dan perpangkatan. Fungsi ini bisa berupa fungsi linear seperti f(x) = ax + b, fungsi kuadrat f(x) = ax² + bx + c, atau fungsi yang lebih kompleks seperti fungsi akar dan pecahan aljabar.

Turunan fungsi aljabar adalah konsep dalam kalkulus yang menunjukkan bagaimana suatu fungsi berubah terhadap variabelnya. Turunan menggambarkan tingkat perubahan atau kemiringan garis singgung pada grafik fungsi tersebut di suatu titik. Turunan fungsi aljabar diperoleh dengan menurunkan pangkat variabel sesuai aturan diferensiasi, misalnya:

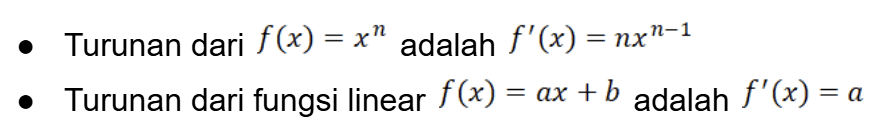
Turunan ini sangat berguna dalam berbagai aspek matematika dan ilmu terapan seperti menentukan kecepatan perubahan, maksimum dan minimum fungsi, serta dalam teknik dan fisika.

 

Limit Fungsi Aljabar

Limit fungsi aljabar adalah nilai yang didekati oleh fungsi tersebut ketika variabelnya mendekati suatu nilai tertentu. Konsep limit ini penting dalam kalkulus karena membantu untuk memahami perilaku fungsi di titik tertentu, terutama ketika fungsi tidak dapat langsung dihitung pada titik tersebut. Secara matematis, limit fungsi f(x) saat x mendekati a dinyatakan sebagai , yang berarti nilai fungsi f(x) mendekati L ketika x mendekati a.

Ada beberapa metode umum untuk menentukan limit fungsi aljabar, antara lain:

• Metode substitusi langsung, mengganti x dengan nilai a jika fungsi terdefinisi pada titik itu.
• Metode pemfaktoran untuk menyederhanakan fungsi agar nilai limit bisa dihitung.
• Metode membagi dengan pangkat tertinggi pada fungsi rasional saat x mendekati tak hingga.
• Metode merasionalkan pembilang atau penyebut jika terdapat akar.

Limit dapat ditentukan dari kedua sisi, yaitu limit kiri (dari arah x mendekati nilai dari sisi kiri) dan limit kanan (dari sisi kanan), dan nilai limit ada jika kedua limit tersebut sama.

Konsep limit ini menjadi dasar dalam pembahasan turunan dan integral dalam kalkulus, serta sangat berguna dalam analisis fungsi dan pemecahan masalah matematika lebih lanjut.

 

Contoh Aljabar Limit Fungsi

Tentukan nilai

Penyelesaian:

Jika substitusi langsung x = 3, bentuknya menjadi , yang tak terdefinisi. Maka, faktorkan pembilang:

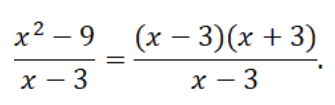
Hilangkan (x – 3) di pembilang dan penyebut, sehingga menjadi x + 3.

Substitusi x = 3, didapat 3 + 3 = 6.

Jadi,

—

Matematika bukan hanya tentang angka, melainkan tentang cara berpikir logis dan sistematis untuk memecahkan masalah dunia nyata. Nah, aljabar adalah pintu gerbangnya. Jika kamu ingin memahami konsep ini dengan cara yang menyenangkan dan aplikatif, yuk bergabung bersama Alta Global School by Ruangguru! 

Di sana, kamu akan belajar tidak hanya “bagaimana cara menghitung”, tetapi juga “mengapa cara itu bekerja”, sehingga pengetahuan matematika kamu menjadi lebih luas, bermakna, dan siap digunakan untuk masa depan.

Alta Global School by Ruangguru menyediakan sistem blended learning, gabungan pembelajaran daring dan luring, mulai dari preschool sampai high school, dengan Champions Curriculum yang menggabungkan kurikulum internasional dan nasional. Yuk, daftar sekarang juga!